高聚物的分子量
高聚物的许多重要性质，如强度、弹性、流动温度、塑性和溶解能力等都与分子量大小有关。但根据反应动力学，由单体经过加聚或缩聚所得合成高聚物，都是不同分子量的同系混合物。大多数天然高分子的分子量也是不均一的。因此，所谓高聚物的分子量，只有统计的意义，是统计平均值。
实际应用上，随所采用方法的不同，所测得的平均分子量也不同，最常用到的平均分子量有数均分子量、重均分子量、粘均分子量和Z均分子量。
1.数均分子量
设高聚物试样中的单体、二聚体、三聚体……i聚体的数目分别为N1、N2、N3……Ni；其各自分子量分别为M1、M2、M3…Mi，将每一分子数乘以其分子量后相加起来，然后除以所有分子总数即得数均分子量。即是分子量按照分子数分布函数N（M）的统计平均。故：
用沸点升高、冰点降低、蒸汽压、渗透压和端基分析等方法可测出数均分子量。
2.重均分子量
将每一级分的重量W与其分子量M的乘积相加后再除以总重量即得重均分子量。即是分子量按照重量分布函数W（M）的统计平均。故:
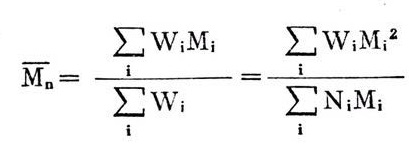
用光散射、扩散和超速离心等方法可给出重均分子量。
3.粘均分子量
可从高聚物在适宜溶剂中的特性粘度来求得，没有物理意义。
4.Z均分子量 分子量按照分数函数MW（M）或M2N（M）的统计平均，它没有具体的物理意义
这种分子量用得不多,可由超离心技术得到这种数据。
图2-1是较典型的高聚物分子量分布和四种平均分子量的比较图。
测定高聚物的方法有许多种,可分为化学法(如端基分析)、热力学法(如沸点上升、冰点下降和渗透压法)、动力学法(如超速离心与沉降及扩散法,粘度法。以及光散射法等其它方法。)测定各种分子量的不同方法及所得平均分子量的统计意义见表2-4。
已发现特性粘度和分子量之间的关系如下所示：
式中K和a是依赖于溶剂和温度的经验常数,a的数值一般在0.5~1.0范围内。
由上述定义可见,各个分子的分子量对用不同方法所测平均分子量所作的贡献是不同。分子量大的分子对M和M的贡献大,而对M的贡献又比对M的大。例如将分子量为0的高分子和分子量为2×104的高分子,各以1克分子相混时,混合物的各种平均分子量分别为:
此处Mv的a值取0.6。由上面计算可见,当高聚物的分子大小不整齐时,其平均分子量有下列顺序:
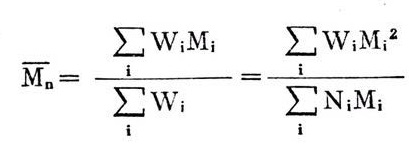
。只有在高聚物的分子量均一的情况下,各种平均分子量才会相等。
